En la Antigüedad, los matemáticos observaron que dados dos triángulos rectángulos con un ángulo agudo común (y por lo tanto los otros dos), al dividir entre si los lados en uno de ellos, los resultados no varían si hacemos las divisiones oportunas en el otro. Y estas divisiones, o razones, sólo dependen del ángulo que fijemos como punto de referencia. Puesto que sólo podemos establecer 6 razones al permutar la hipotenusa y los catetos en el numerador y el denominador de la fracción, tenemos 6 razones inmutables.Sea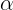 
el ángulo agudo en cuestión. Al cateto que no forma parte del lado del ángulo (b) se le llama cateto opuesto y contiguo al que si forma parte del mismo (c). Denotando por a, a la hiponesusa, podemos dar nombre a estas 6 cantidades: las razones trigonométricas del ángulo :
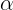Podemos generalizar las razones trigonométricas a cualquier ángulo, identificando la abscisa (x) y la ordenada (y) con el coseno y el seno respectivamente. Y para jugar con todo esto, os dejo este aplet que espero os guste.
Hay una página de Solucionarios de Matemáticas que te puede interesar
ResponderEliminarComo se hace este modelo en excel?
ResponderEliminarHola voy a utilizar las fórmulas presentadas para resolver un ejercicio propuesto.
ResponderEliminarEjercicio:
Dado un triángulo rectángulo donde el cateto opuesto mide 4 unidades y el cateto adyacente mide 3 unidades. Calcular el valor exacto de las razones trigonométricas seno, coseno y tangente para este triángulo.
Comenzando por Seno (sen)
sen∝ =(cateto opuesto)/hipotenusa
sen ∝ =4/hipotenusa
Utilizando el teorema de Pitágoras para obtener el valor de la hipotenusa
c^2 =a^2+b^2
c^2 =3^2+4^2
c^2 =9+16
c =√25
c =5
Retomando las razones trigonométricas
sen ∝ =4/5
Ahora para Coseno (cos)
cos∝ =(cateto adyacente)/hipotenusa
cos∝ =3/5
Resolviendo para Tangente (tan)
tan∝ =(cateto opuesto)/(cateto adyacente)
tan∝ =4/3
Por lo tanto, las razones trigonométricas para el ejercicio propuesto son
sen ∝ =4/5
cos∝ =3/5
tan∝ =4/3
Teniendo en cuenta las razones trigonométricos podemos determinar la identidad Pitágorica se la siguiente manera,
ResponderEliminarTeniendo un triángulo rectángulo cuya hipotenusa es igual a 1 y tenemos al cateto a siendo este el opuesto al ángulo con el que estamos trabajando y b como cateto adyacente tenemos:
Sen(∝) =a/1 = a
Cos(∝) =b/1 = b
Teniendo que la identidad Pitágorica queda:
Sen²(∝) + cos²(∝) = 1²
Las razones trigonométricas son fundamentales en trigonometría y tienen aplicaciones extensas en matemáticas, física, ingeniería y muchas otras áreas.
ResponderEliminar______________________________________________
Soy maestro en la Escuela Bancaria Comercial