Aunque este post surgió hace varios años, las coincidencias que hacen que los astros se alineen, me han decidido a escribirlo.
El estudio de las proporciones, aplicado a la Arquitectura, da lugar a bellas composiciones que con el paso del tiempo permanecen olvidadas aunque inalterables en forma de piedra. Este es el caso de un gran número de Catedrales y edificios singulares de los siglos XVI y XVII.
 |
| Puerta Principal de la Catedral de Almería |
El caso que nos ocupa, es la Catedral-Fortaleza de la Encarnación en Almería, Su construcción dio comienzo a partir de 1522 con una doble función: dar amparo moral a los cristianos y protegerlos de las insurrecciones moriscas así como de los piratas berberiscos que asolaban el Mediterráneo. Dado que la construcción del templo finaliza en 1564 por Juan de Orea, incorpora elementos tanto góticos como renacentistas.
El estilo renacentista, toma muchos y variados ejemplos de la cultura Helénica, como es la utilización del número áureo así comos otro irracionales (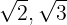 ) que dan lugar a rectángulos cuyos lados guardan estas proporciones. Para la obtención del número de oro, tenemos que recurrir a la división en media y extrema razón de un segmento:
) que dan lugar a rectángulos cuyos lados guardan estas proporciones. Para la obtención del número de oro, tenemos que recurrir a la división en media y extrema razón de un segmento:
"Diremos que un segmento se encuentra dividido en media y extrema razón, si la medida mayor es media proporcional entre el total y la parte menor". Es decir, dado un segmento de longitud 1 (suposición que no resta generalidad, pues en otro caso basta con buscar el correspondiente homotético) y la longitud del lado mayor sea x. Entonces:
De estas dos soluciones, al descartar la negativa, llamamos número de oro a la restante, es decir:
Veamos cómo se realiza la construcción de los rectángulos áureo, es decir, aquellos en los que la razón de sus lados es 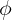 :
:
Partimos de un cuadrado ABCD, de lado l, y marcamos el punto medio de uno de sus lados, dígase E. Con centro en este punto, y radio la distancia de E a C, trazamos un arco de circunferencia que cortará a la prolongación del lado AB en el punto F. El rectángulo AFGD, es áureo.
Para demostrar lo que se afirma, basta con calcular la dimensión del lado AF y comprobar que la razón que forma junto al lado AD, es 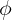
Así:
En el caso de los rectángulos 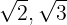 , las construcciones son similares, salvo que el centro de la circunferencia es un vértice del cuadrado (en el primer caso) y en el segundo un vértice de un rectángulo cuya base es el doble de la altura.
, las construcciones son similares, salvo que el centro de la circunferencia es un vértice del cuadrado (en el primer caso) y en el segundo un vértice de un rectángulo cuya base es el doble de la altura.
Y para que el lector pueda descubrir los rectángulos anteriores, en el Templo almeriense, sólo tiene que jugar con el siguiente aplet de Geogebra:
Los más excépticos, quizá puedan achacarme que el método empleado, no constituye una demostración, pero sigue la misma metodología expuesta por el profesor de la Universidad de Granada Álvaro Martínez Sevilla, en sus paseos matemáticos por Granada, a quien tuve el gusto de conocer en el V Encuentro de Geogebra celebrado en Málaga y divertirme con sus explicaciones.
¿Es necesario coger instrumentos de medida para comprobar la presencia de la proporción áurea en los monumentos? La respuesta es no; cuando pases frente a ellos, coje tu DNI (que también es un rectángulo áureo) y cerrando un ojo házlo coincidir con los que aparecen marcados en las fotografías en dorado; verás que son semejantes. Cuando el lector pasee por el centro de su ciudad, ya tiene un nuevo entretenimiento: buscar la proporción áurea. Adelante, que hay bastantes más ejemplos.
Este post participa en la Edición 8.3 del Carnaval de Matemáticas cuyo anfitrión es el Blog Semillas.