Aprovechando las nuevas herramientas que he aprendido en el curso que estoy finalizando, Geogebra Avanzado, que organiza la SAEM Thales he construido un applet en el que se explica la construcción de la tesela hueso nazarí. Espero que la disfrutésis y cuando tengáis ocasión de visitar la Alhambra de Granada lo podáis ver decorando las paredes de los Palacios Nazaríes
Esta es una ventana para que podáis ver lo que hago y por lo que tengo pasión.
Mi lista de blogs
miércoles, 3 de diciembre de 2014
jueves, 18 de septiembre de 2014
Infidelidades matemáticas
Hablar de Matemáticas
y exactitud, puede parecer sinónimo; en cambio, los resultados matemáticos no
siempre tienen precisión cuando nos referimos a sus descubridores. Veremos que
hay nutridos e importantes ejemplos en los que se atribuyen teoremas a
matemáticos, que si bien en ocasiones han contribuido a su demostración o los
han redescubierto más tardíamente, en otro casos nunca nada tuvieron que ver
con ellos.
Puesto que este post se plantea interrogantes léxicos, quizás la Lingüística nos sirva para
poner luz sobre las dudas anteriormente planteadas. El adjetivo epónimo, hace alusión al «
nombre de una persona o de un lugar que designa un pueblo,
una época, una enfermedad, una unidad, etc.». Usando este vocablo,
podemos en lo sucesivo hablar de epónimos para referirnos a los resultados que
son acompañados del nombre del descubridor
por el que se les conoce.
Fundamentalmente hay
dos formas de crear los epónimos:
- Asociando el nombre de la persona o el lugar con el significado del epónimo dando así lugar a una lexía compleja, mediante el uso del genitivo de (Teorema de Pitágoras, Regla de Laplace,...)
- Utilizar el nombre del descubridor, como raíz para formar adjetivos (Geometría euclidiana, anillo noetheriano,...). En ocasiones, el epónimo permite una elipsis léxica simplificando la escritura (matriz hessiana por Hessiano o abeliano por grupo abeliano).
Enriquecido nuestro vocabulario matemático, demos una vuelta de tuerca al planteamiento
inicial. Stephen M. Stigler, profesor de Estadística en la Universidad de
Chicago, formuló la llamada Ley de eponomía según la cual «ningún descubrimiento científico lleva el nombre de su descubridor
original» (Stigler ,1980). En este artículo, se dan a conocer
ejemplos en diversos ámbitos de las Ciencias, y reconoce que antes que él, el
sociólogo Robert K. Merton había formulado otra hipótesis en un sentido similar
al suyo, y que esgrime que «todos
los descubrimientos científicos tienen principios múltiples» y que los científicos con mayor prestigio suelen tener mayor
reconocimiento que otros de menor talla, por lo que suele a los primeros
atribuírseles los galardones. Esta posición se conoce con el nombre de efecto Mateo, epónimo que se debe al
evangelista Mateo. En la parábola del Sembrador afirma que «a cualquiera que tiene, se le dará, y tendrá más; pero al que no
tiene, aún lo que tiene le será quitado».
Surge de manera
natural la siguiente cuestión: ¿Quién merece el título de un teorema? ¿Quien lo
usa por primera vez? ¿Quien lo publica? ¿Quien lo demuestra? Sin entrar en
juicios de valor, lo cierto es que cada vez más encontramos resultados en los
que aparecen varios de los nombres de sus descubridores. Sirvan como ejemplo
los teoremas de Gauss-Bonet en Geometría Diferencial que relaciona la curvatura
de Gauss de una superficie con su característica de Euler, la desigualdad de Cauchy-Schwarz aplicada en
diversos campos, o los métodos de Runge-Kutta para resolver ecuaciones
diferenciales en el ámbito del Análisis Numérico.
La precisión de los
contenidos matemáticos, es una de las características más destacables de la
disciplina. A lo largo del s. XX, la introducción de los ordenadores para
realizar cálculos, ha hecho que el Cálculo Numérico se desarrolle, dando
soluciones aproximadas a problemas que de manera exacta no sabemos resolver.
Pero, en cualquier caso, estos resultados van acompañados de una medida del
error que se comete al tomar como solución una aproximación de la misma. Esta
visión macroscópica hace que, para profanos y doctos, la Matemática sea una Ciencia Exacta .
Vamos a poner de
manifiesto mediante diversos ejemplos, cómo el devenir del tiempo deja huecos en las
identidades de los descubridores de algunos resultados, atribuyéndolos a otros
que en ocasiones nada han tenido que ver con la investigación sobre estos
teoremas. En casos más leves, los autores de los mismos los han redescubierto,
incluso dando una demostración de ellos, quedando en el olvido su origen. Los que aquí nos competen, los denominaremos epónimos infieles, pues mostraremos que la Historia les ha hecho un
flaco favor a sus creadores.
Epónimos
infieles
- El Triángulo de Releaux.
El ingeniero
mecánico alemán Franz Releaux (1829-1905), desarrolló los llamados polígonos de
Releaux, que se caracterizan por ser de anchura constante. El ejemplo más
simple, es el Triángulo de Releaux, que encontramos como motivo utilizado en la arquitectura gótica (últimos siglos de la Edad Media).
- El teorema de Pitágoras
La famosísima relación entre los lados de un triángulo rectángulo, era conocida bastantes siglos antes de Pitágoras (ca. 569 a. C. – ca. 475 a. C) por los Bablinonios. Una prueba de ello lo encontramos en una tabla de arcilla, conocida como Plimtom 322 , que pudo ser escrita en el 1800 a. C. y en la que aparecen ternas pitagóricas (eso si, hay que traducirlas a nuestro sistema decimal, pues se encuentran escritas en base 60 y con la grafia de sus creadores).
- Números arábigos
El sistema
de numeración posicional que actualmente usamos y las grafías de los números
empleados, son comúnmente conocidos bajo el epónimo de arábigos; en cambio, su
origen es hindú. Podemos asimismo, encontrarlos bajo el nombre de
indo-arábigos, pues como también encontramos erróneamente en numerosos textos «son los árabes los que introducen la grafía del cero».
- Triángulo de Pascal
Esta ordenación de números, que nos permite de una forma cómoda calcular números combinatorios de un orden pequeño, recibe el nombre del eminente matemático francés Blaise Pascal (1623 - 1662). En Italia recibe el de Triángulo de Tartaglia. Pero en el 200 a. C. , en China ya se conocía este resultado, así como durante la Edad Media en Persia.
- Binomio de Newton
No podía ser Sir Isaac Newton (1643 - 1727) menos que Pascal y tener su epónimo infiel. En efecto, el resultado fué descubierto por Abu Bekr ibn Muhammad ibn al-Husayn al-Karaji alrededor del año 1000.
- Teorema de Napoleón
El que fuese emperador de Francia y dueño de casi toda Europa, Napoleón Bonaparte, da nombre a un resultado en Geometría:
Si se construyen tres triángulos equiláteros a partir de los lados de un
triángulo cualquiera, todos al interior o todos al exterior, entonces
los centros de los triángulos equiláteros forman también un triángulo
equilátero.
Como podemos leer en el blog de Tio Petros, y aunque Napoleón fuese un gran aficionado por las Matemáticas, la demostración de este resultado hay que situarla en Lorenzo Mascheroni.
La lista de epónimos infieles, sería enorme (y deberían estar todos los resultados si nos dejamos convencer por Stigler). Podéis seguir buscando, porque lo cierto es que hay muchos más.
Esta entrada participa en la Edición 5.6: Paul Erdős del Carnaval de Matemáticas, cuyo anfitrión es el blog Cifras y Teclas.
sábado, 31 de mayo de 2014
Propuesta didáctica con la alfombra de Sierspinski
El reconocimiento del trabajo desarrollado por José Luis Rodríguez Blancas hace dos años en el concurso internacional Ciencia en Acción, donde consiguió la primera mención de honor con el proyecto titulado "Geometría flexible y topología con el mago Moebius" y el primer premio ex aequo el año pasado "Trenzados árabes con cuerdas", nos ha animado a presentar un proyecto a la XV edición que tendrá lugar en Barcelona del 3 al 5 de Octubre de 2014. Esta vez, la propuesta se titula "Juegos y joyas fractales" y aborda el estudio de estos objetos geométricos de una forma globalizada: tanto en el sentido de los contenidos tratados, como en el arco de edades a los que van dirigidas las actividades. La viabilidad del proyecto, se ve sustentada por el equipo humano que lo compone, como se puso de manifiesto en la pasada edición de la Feria de la Ciencia en Sevilla.
En esta entrada voy a describir una propuesta didáctica que hemos realizado en el CEIP Francisco de Goya. Nos hemos marcado como objetivo presentar a los niños el concepto de fractal a través de una característica destacable a simple vista: la autosimilitud. Para ello, hemos planteado la construcción de la alfombra de Sierpinski con niños de infantil de 4 y 5 años, usando gomets (pegatinas de colores).
Características del fractal
Este fractal es la versión plana de la esponja de Menger y se construye dividiendo un cuadrado en otros nueve y eliminando el central. Por lo tanto, en cada paso aparecen 8 copias con lado 1/3 de la iteración anterior. De esta forma, su dimensión fractal es:

Pero no sólo es interesante el hecho de que su dimensión sea un número irracional; más sorprendente aún es el hecho de tener perímetro infinito y... superficie nula. Veamos que estas afirmaciones son ciertas:
Partimos de un cuadrado de lado  y sean
y sean 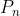 y
y 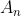 el perímetro y el área del fractal, respectivamente, en la iteración n. Entonces tenemos:
el perímetro y el área del fractal, respectivamente, en la iteración n. Entonces tenemos:
Tomando límites en la última expresión del perímetro, aparece una serie geométrica con razón
y por lo tanto es divergente, lo que prueba lo postulado para el perímetro.
Respecto del área, podemos razonar sustrayendo al área del cuadrado original la de los cuadrados centrales. En cambio, resulta más cómodo considerar que en cada iteración el número de cuadrados se ve multiplicado por 8 y el lado de los mismos es la tercera parte. Así:
Tomando nuevamente límite en esta última expresión, resulta que tiende a cero, con lo que la alfombra tiene área nula. Es decir, tiende a no verse.
Realización de la actividad
La construcción anterior para el cálculo del área, nos hace recapacitar sobre el número de cuadrados que componen cada una de las iteraciones. Así, en el paso n, necesitamos 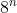 cuadrados. Como nuestra propuesta ha sido construir la cuarta iteración, hemos necesitado
cuadrados. Como nuestra propuesta ha sido construir la cuarta iteración, hemos necesitado 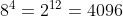 cuadraditos. Concretamente hemos usado gomets de 2 cm de lado y para facilitar el montaje, les hemos proporcionado a los niños una plantilla de la primera iteración sobre la que pegarlos. Una vez recortados los cuadrados de la primera iteración, y agrupados por parejas, se han pegado sobre un A4 previamente cortado a la medida necesaria (cuadrado de 19,4 cm de lado, ya que se ha dejado una tolerancia de 1 mm por cada gomet) 8 cuadrados de la primera iteración, conformando de esta forma la segunda.
cuadraditos. Concretamente hemos usado gomets de 2 cm de lado y para facilitar el montaje, les hemos proporcionado a los niños una plantilla de la primera iteración sobre la que pegarlos. Una vez recortados los cuadrados de la primera iteración, y agrupados por parejas, se han pegado sobre un A4 previamente cortado a la medida necesaria (cuadrado de 19,4 cm de lado, ya que se ha dejado una tolerancia de 1 mm por cada gomet) 8 cuadrados de la primera iteración, conformando de esta forma la segunda.
El resto es cosa de paciencia, pegamento y buen hacer de las Maestras (y el maestro) con los niños. El resultado es el siguiente:
 | ||||
| Infantil 4 años |
 | |
| Infantil 5 años |
Queremos reconocer la encomiable labor que han realizado las Maestras de Infantil, así como el interés mostrado para poder realizar esta actividad. Especialmente quisiera, otra vez, agradecer a la Seño Isabel Salmerón su implicación en la Educación de sus alumnos.
Podéis ver más información de las actividades en las siguientes direcciones:
martes, 20 de mayo de 2014
Feria de la Ciencia
Este año, nuevamente he tenido la oportunidad de participar en este evento. El proyecto presentado se titula Juegos y joyas fractales y han participado en el mismo el IES Francisco Montoya, el CEIP San Fernando, el Centro Educativo Agave y la Universidad de Almería. De la mano de José Luis Rodríguez Blancas, un equipo de profesores formado por Lola Jiménez, Lidia García, Mari Carmen Sánchez y el que escribe, llevamos varios meses preparando con mucha ilusión los materiales que hemos presentado:
- La curva de Hilbert, un fractal que recorre todos los puntos del cuadrado unidad.
 |
| En esta fotografía, se puede ver el proceso de construcción de la 4ª iteración, usando unas plantillas con clavos que permiten su trazado |
- La segunda iteración de la esponja de Menger con polifieltros 3D.
 |
| Esta imagen, muestra el proceso de montaje de la misma |
- La cuarta iteración del tetraedro de Sierspinski usando módulos triangulares de papiroflexia.
- El fractal pitagórico (undécima iteración).
En esta foto, nos acompaña Pepe Muñoz (Grupo Alquerque). Gracias a su trabajo sobre papiroflexia para la X Feria de la Ciencia, pude empezar con este recurso que se ha convertido en algo indispensable y que me produce gran satisfacción.
El collar que lleva Lidia, es una de las joyas que José Luis Rodríguez hizo para mostrar cómo un fractal, es también una joya. No os perdáis la entrada a su blog.
El proyecto, a juzgar por los comentarios de los visitantes, nos hace pensar que ha sido todo un éxito. Este acicate nos permite seguir con la ilusión con la que empezamos esta edición y nos anima a continuar en esta linea de trabajo. Lo cierto es que sin un equipo humano tan involucrado, es difícil llevar a buen puerto una empresa de esta entidad. Por lo tanto, quiera nuevamente, felicitaros por vuestra labor. Como no quiero dejarme a nadie por el camino, hago extensivo este agradecimiento a la comunidad educativa y a la dirección de los centros implicados en el mismo. Especialmente no quiero olvidar a mis alumnos, que han trabajado con ilusión y tenacidad para que el proyecto fuese viable.
lunes, 31 de marzo de 2014
Resumen Edición 5.2: Emmy Noether
Finalizado el plazo para la participación en la Edición 5.2: Emmy Noether del Carnaval de Matemáticas, toca hacer recuento de las mismas. La nueva experiencia de ser anfitrión de esta edición, ha sido muy intensa, ya que la producción de algunos blogeros es... infinita y más allá. Las entradas que me habeis comunicado al correo o al blog, he procurado dar acuse de recibo de las mismas y agradeciendo la participación. En las más nuevas, el trabajo del fin de semana en la L Edición de la Olimpiada Matemática Española en la ciudad de Requena, me ha consumido una parte importante de los recursos y no he podido dirigirme a los participantes.
Sin más dilación, paso a relacionar los participantes en esta edición del Carnaval:
- Conociendo frutas y verduras desde Planilandia, aportado por ZTFNews.org
- El juego del jazz aportado por ZTFNews.org
- PIkasle’s Mathematics, Magic and Mystery Workshop aportado por ZTFNews.org
- Grace Chisholm Young aportado por ZTFNews.org
- Noventa años sin García de Galdeano aportado por ZTFNews.org
- Möbius ‘strip’, digo ‘strap’ aportado por ZTFNews.org
- Día Mundial del Teatro, con Émilie aportado por ZTFNews.org
- Centenario del nacimiento de Toru Kumon aportado por ZTFNews.org
- PiClock, eso mismo, un pi-reloj aportado por ZTFNews.org
- El legado de las matemáticas griegas… en dos minutos aportado por ZTFNews.org
- Dos más dos son, según Adam Ries, cuatro aportado por ZTFNews.org
- La t de Student aportado por pimedios
- Cristales y Matemáticas aportado por pimedios
- El voraz algoritmo de Sylvester aportado por pimedios
- Pompas de jabón. La belleza de las Matemáticas aportado por Juan Bragado.
- Un puzzle sencillo aportado por culturacientifica.com
- La probabilidad y el amanecer aportado por Matifutbol
- Si nunca ha pasado, ¿qué probabilidad hay de que pase? aportado por Blioquinfo
- Jugando con un almanaque aportado por matemasticasmaldonado
- Información, probabilidad, bits, el juego de las preguntas y las entropías aportado por cienciaonline
- XXX Olimpiada Matemática Thales aportado por elmundoderafalillo
- ¿Cuántos huevos Kinder tendré que comer? aportado por Blioquinfo
- Topología Bilbaína aportado por Pikasle
- Premio#CarnaMat51 aportado por Tito Eliatron Dixit
- La paradoja de la copa de Martini...integral aportado por Naukas
- El Istikmal de Al Mutamán aportado por Guirnalda matemática
- Matemáticas y animación 3D: un proceso creativo aportado por Tito Eliatron Dixit
- Membrana N-Luz Objetos N-Luz aportado por Icaraideas
- Media armónica focal aportado por Guirnalda matemática
- ¿Figuras fractales con octaedros truncados? enviado por Juegos Topológicos
- Henry Moore enviado por High Ability Dimension
- II Día de las Matemáticas en el IES Chaves Nogales enviado por i-matematicas.com
- Matemáticas gamberras enviado por Los matemáticos no son gente seria
- ¿Qué narices es el cero? enviado por Scire Science
- Usemos un nuevo juguete: el cero enviado por Scire Science
Ya sólo me queda (si no me he dejado a nadie, que aunque espero que no, podría ser) animaros a la lectura de los post y a que elijáis el que más os guste. Para ello teneis hasta el día 16 de abril.
Mucha suerte a todos los participantes y enhorabuena por el nivel de las publicaciones.
lunes, 10 de marzo de 2014
Edición 5.2: Emmy Noether
Me complace anunciaros que este blog es el anfitrión del mes de marzo del Carnaval de Matemáticas. Esta edición que es la número 42, y siguiendo la sugerencia del blog pimedios, lleva el nombre de un matemático que tenga alguna efeméride en el mes de marzo. El pasado sábado 8 de marzo, se celebró el día internacional de la mujer y me parecía importante que fuese una mujer la que diese título a esta edición de la que alberga mi blog.
Emmy Noether, fue una matemática de origen judío, nacida en Erlangen (Alemania) el 23 de marzo de 1882, cuyos trabajos versaron sobre Física Teórica y Álgebra Abstracta. Aunque cursó estudios para ser profesora de inglés y francés, los antecedentes familiares nutridos de matemáticos (entre los que se encontraba su padre que era profesor en la Universidad de Erlangen y sucesor en el puesto de Felix Klein) hicieron que se decantara por esta disciplina.
La homofobia reinante, hacía que las mujeres no pudieran matricularse en las Universidades y sólo extraoficialmente podían asistir como oyentes si el profesor de turno les concedía esta gracia. De esa singular manera, pudo Emmy recibir clases de mano de su padre en Erlangen. Un cambio en las leyes de admisión del alumnado, hizo que Noether pudiese acceder al doctorado y publicar su tesis con un trabajo sobre invariantes en 1907.
Su excepcional talento permitió que en 1915 pusieran sobre ella sus miradas David Hilbert y Klein, para que participase de sus proyectos en la Universidad de Göttingen. Allí, otra vez producto del rechazo hacia las mujeres, tuvo que impartir clase sin recibir a cambio ningún estipendio hasta 1919, en que finalmente recibió la aprobación para ejercer como profesora remunerada.
La ascensión de Adolf Hitler al poder en 1933 hizo que se proclamaran leyes antisemitas que impidieron a Noether continuar con su labor docente. Por este motivo, se trasladó a la Universidad de Bryn Mawr, en Pensilvania (EEUU), donde murió el 14 de abril de 1935, días después de haber sido sometida a una intervención quirúrgica.
Por último, vamos a recordar las normas de participación en el Carnaval:
Tienes que escribir una entrada en tu blog sobre algún contenido que verse sobre Matemáticas (y cuando digo algún, puede ser una foto) durante el periodo en que se encuentra abierta la edición del mismo, es decir, del 24 al 30 de marzo. En la misma, debes mencionar que tu post participa en
la presente edición e incluir un vínculo al blog anfitrión Matesdedavid y la web del Carnaval de Matemáticas. A modo de referencia puede ser:
Esta entrada participa en la Edición 5.2 del Carnaval de Matemáticas cuyo anfitrión es Matesdedavid
Para tener un registro de las entradas y hacer más fácil la labor administrativa, se ofrecen tres posibilidades:
- Dejando una reseña de tu entrada en la web del Carnaval.
- Mediante un comentario en esta misma entrada con un link a tu aportación.
- Por correo electrónico a davidcasteleiro@hotmail.com.
Gracias a todos los que haceis posible este Carnaval.
Suscribirse a:
Entradas (Atom)








