 Estos días de confinamiento obligado me han permitido leer
sin cortapisas, una de mis aficiones más introspectivas. A falta de poder salir a la calle echando de menos ver el mar de cerca, el monotema que nos tiene absortos es el COVID-19 o coronavirus. Las noticias sobre él, alarmantes por momentos, se jalonan de algunas
barbaridades que un matemático no puede leer sin que le piten los oídos.
Estos días de confinamiento obligado me han permitido leer
sin cortapisas, una de mis aficiones más introspectivas. A falta de poder salir a la calle echando de menos ver el mar de cerca, el monotema que nos tiene absortos es el COVID-19 o coronavirus. Las noticias sobre él, alarmantes por momentos, se jalonan de algunas
barbaridades que un matemático no puede leer sin que le piten los oídos.
Algunos rotativos insignes, como La Vanguardia
(https://www.lavanguardia.com/vida/20200316/474186615740/evolucion-curva-coronavirus-por-comunidad-autonoma.html) afirman que
(https://www.lavanguardia.com/vida/20200316/474186615740/evolucion-curva-coronavirus-por-comunidad-autonoma.html) afirman que
“los casos nuevos de Covid-19 no paran de aumentar día tras día. La curva de crecimiento es exponencial: incrementó de 0 a 100 en la primera semana, de 100 a 1.000 en la segunda semana y en la tercera semana todo apunta que se llegará a los 10.000.”
Y claro, con la patente de corso de las Matemáticas y la
Ciencia, cualquiera emite juicios sumarísimos que nuestras tragaderas tienen
que aceptar; o no. Si un plumilla debe tener cerca un diccionario para
consultar sus dudas léxicas, próximo debería tener a un matemático al hablar de una disciplina que quizá ni cursó en el Bachillerato.
Veamos cuáles son las dos grandes falacias de enunciados
como estos:
1. Crecimiento exponencial.
La función exponencial es una función real de variable real, considerada dentro del grupo de las elementales. Elementalmente, cualquier
titulado en ESO y qué no decir de los Licenciados Vidriera que tienen a
bien llenar las páginas de los periódicos y parrillas televisivas, debería
conocerla. Se define cuando la base es un número real positivo, 1. Crecimiento exponencial.
Claramente, dependiendo del valor que tome la base, la naturaleza de la función es distinta pudiendo ser decreciente si 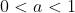 o creciente cuando
o creciente cuando 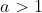 .
.

Aunque el lenguaje a veces pueda parecer excesivo, en un momento en el que se propugna el inclusivo y eternizamos las disertaciones con ellos y ellas, también debería se inclusivo el rigor para hablar de crecimiento exponencial de base mayor que 1.
2. Modelo exponencial para cuantificar los
infectados.
Si bien es cierto que localmente el crecimiento de la población de infectados puede tener un comportamiento que se asemeje a una función exponencial de base mayor que uno, este modelo se vuelve inconsistente ya que no tiene en cuenta las personas que curan de la enfermedad, ni las medidas de aislamiento.
En efecto, consideremos la siguiente tabla que muestra el número de infectados en España hasta el 17 de marzo:
| Día | Casos confirmados | Activos | Recuperados | Muertos |
|---|---|---|---|---|
| 31 de enero | 1 | 1 | 0 | 0 |
| 9 de febrero | 2 | 2 | 0 | 0 |
| 13 de febrero | 3 | 2 | 0 | 1 |
| 24 de febrero | 4 | 3 | 0 | 1 |
| 25 de febrero | 8 | 7 | 0 | 1 |
| 26 de febrero | 14 | 13 | 0 | 1 |
| 27 de febrero | 26 | 25 | 0 | 1 |
| 28 de febrero | 45 | 44 | 0 | 1 |
| 29 de febrero | 59 | 58 | 0 | 1 |
| 1 de marzo | 84 | 83 | 0 | 1 |
| 2 de marzo | 125 | 124 | 0 | 1 |
| 3 de marzo | 169 | 167 | 0 | 2 |
| 4 de marzo | 228 | 224 | 1 | 3 |
| 5 de marzo | 282 | 276 | 3 | 3 |
| 6 de marzo | 365 | 347 | 10 | 8 |
| 7 de marzo | 430 | 10 | ||
| 8 de marzo | 674 | 17 | ||
| 9 de marzo | 1231 | 30 | ||
| 10 de marzo | 1695 | 36 | ||
| 11 de marzo | 2277 | 55 | ||
| 12 de marzo | 3146 | 86 | ||
| 13 de marzo | 5232 | 4906 | 193 | 133 |
| 14 de marzo | 6332 | 5603 | 517 | 193 |
| 15 de marzo | 7844 | 7035 | 517 | 292 |
| 16 de marzo | 9942 | 9070 | 530 | 342 |
| 17 de marzo | 11178 | 9659 | 1028 | 491 |
donde x denota el número de días transcurridos desde el 23 de febrero y f(x) el de personas infectadas.
Resolviendo una elemental ecuación, para determinar si es posible que toda la población que vive en nuestro país (47 100 396 en el segundo semestre de 2019) se va a infectar, resulta que:
Es decir, el 12 de abril estaremos todos infectados (el refrán español de aquí a 100 años todos calvos, tiene una versión vírica con 48 días).
Pero si el lector trata de extrapolar la función para ver cuál es su predicción con la población mundial, el 24 de abril estaríamos todos coronados.

Este comentario ha sido eliminado por el autor.
ResponderEliminarHola
ResponderEliminarHola
ResponderEliminarHola
ResponderEliminarMuchas gracias por el aporte
ResponderEliminar_________________________________________
Soy profesor de licenciaturas ejecutivas una universidad en México