El reconocimiento del trabajo desarrollado por José Luis Rodríguez Blancas hace dos años en el concurso internacional Ciencia en Acción, donde consiguió la primera mención de honor con el proyecto titulado "Geometría flexible y topología con el mago Moebius" y el primer premio ex aequo el año pasado "Trenzados árabes con cuerdas", nos ha animado a presentar un proyecto a la XV edición que tendrá lugar en Barcelona del 3 al 5 de Octubre de 2014. Esta vez, la propuesta se titula "Juegos y joyas fractales" y aborda el estudio de estos objetos geométricos de una forma globalizada: tanto en el sentido de los contenidos tratados, como en el arco de edades a los que van dirigidas las actividades. La viabilidad del proyecto, se ve sustentada por el equipo humano que lo compone, como se puso de manifiesto en la pasada edición de la Feria de la Ciencia en Sevilla.
En esta entrada voy a describir una propuesta didáctica que hemos realizado en el CEIP Francisco de Goya. Nos hemos marcado como objetivo presentar a los niños el concepto de fractal a través de una característica destacable a simple vista: la autosimilitud. Para ello, hemos planteado la construcción de la alfombra de Sierpinski con niños de infantil de 4 y 5 años, usando gomets (pegatinas de colores).
Características del fractal
Este fractal es la versión plana de la esponja de Menger y se construye dividiendo un cuadrado en otros nueve y eliminando el central. Por lo tanto, en cada paso aparecen 8 copias con lado 1/3 de la iteración anterior. De esta forma, su dimensión fractal es:
Pero no sólo es interesante el hecho de que su dimensión sea un número irracional; más sorprendente aún es el hecho de tener perímetro infinito y... superficie nula. Veamos que estas afirmaciones son ciertas:
Partimos de un cuadrado de lado 
y sean 
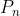y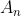 
el perímetro y el área del fractal, respectivamente, en la iteración n. Entonces tenemos:
Tomando límites en la última expresión del perímetro, aparece una serie geométrica con razón
y por lo tanto es divergente, lo que prueba lo postulado para el perímetro.
Respecto del área, podemos razonar sustrayendo al área del cuadrado original la de los cuadrados centrales. En cambio, resulta más cómodo considerar que en cada iteración el número de cuadrados se ve multiplicado por 8 y el lado de los mismos es la tercera parte. Así:
Tomando nuevamente límite en esta última expresión, resulta que tiende a cero, con lo que la alfombra tiene área nula. Es decir, tiende a no verse.
Realización de la actividad
La construcción anterior para el cálculo del área, nos hace recapacitar sobre el número de cuadrados que componen cada una de las iteraciones. Así, en el paso n, necesitamos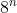 
cuadrados. Como nuestra propuesta ha sido construir la cuarta iteración, hemos necesitado 
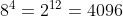cuadraditos. Concretamente hemos usado gomets de 2 cm de lado y para facilitar el montaje, les hemos proporcionado a los niños una plantilla de la primera iteración sobre la que pegarlos. Una vez recortados los cuadrados de la primera iteración, y agrupados por parejas, se han pegado sobre un A4 previamente cortado a la medida necesaria (cuadrado de 19,4 cm de lado, ya que se ha dejado una tolerancia de 1 mm por cada gomet) 8 cuadrados de la primera iteración, conformando de esta forma la segunda.
El resto es cosa de paciencia, pegamento y buen hacer de las Maestras (y el maestro) con los niños. El resultado es el siguiente:
 | ||||
| Infantil 4 años |
 | |
| Infantil 5 años |
Queremos reconocer la encomiable labor que han realizado las Maestras de Infantil, así como el interés mostrado para poder realizar esta actividad. Especialmente quisiera, otra vez, agradecer a la Seño Isabel Salmerón su implicación en la Educación de sus alumnos.
Podéis ver más información de las actividades en las siguientes direcciones:
No hay comentarios:
Publicar un comentario