Hace una fechas, me topé con una de estas imágenes que circulan por las redes, en las que se ve un cuadrado subdividido y hacen la preguntita ¿Cuántos cuadrados ves? Al tratar de resolverlo, debes seguir alguna estrategia y en este caso, basta con contar. Tomemos como unidad, la medida del lado más pequeño y podemos contar cuántos hay de cada tipo. Veamos un ejemplo, donde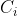 
, denota el número de cuadrados que hay en uno, de tamaño i:
Y aquí vino mi sorpresa: ¡el número de cuadrados, se puede a su vez expresar como la suma de cuadrados de naturales consecutivos! Tan bonito resultado, no le queda más remedio que ser cierto y no fruto de la casualidad de estos primeros casos. Y en efecto es así. Para demostrarlo, pensemos que un cuadrado de tamaño mayor, se obtiene adosándole una orla al de tamaño inmediatamente anterior, como podemos ver en el siguiente dibujo:
Y aquí, la Geometría se fusiona con el Análisis, para las cuentas. Claramente, el número de cuadrados, será el que haya en uno de tamaño inferior, junto con los nuevos que genere la orla. Denotando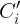 
al número de cuadrados nuevos, se tiene: 
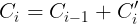, para i cualquier natural superior a uno.
Queremos demostrar que 
(*). Además, esta suma no cuesta mucho demostrar que se puede expresar como:
Manos a la obra: para demostrar que el número de cuadrados es una suma de cuadrados como en (*), procedemos por inducción:
- Para n=1, claramente se tiene la igualdad
- Supongamos cierta la igualdad para un natural n.
- Para n+1:
Veamos entonces cuántos cuadrados nuevos se generan con la orla. Para ello, vamos a considerar el lado de los mismos:
- De lado 1: (n+1) + n = 2n+1
- De lado 2: n + (n-1) = 2n-1
- De lado 3: (n-1) + (n-2) = 2n-3
...................................................
- De lado n: 2 + 1 = 3
- De lado n+1: 1
_________________________________________________
En total:
Pero la suma, es la de los n+1 términos de una progresión aritmética de diferencia 2, con lo que aplicado la consabida fórmula, se tiene:
lo que concluye la demostración.
Así, en número de cuadrados que "ves" en uno de lado n, viene dado por:
¿No es sencillamente precioso?
El problema de "¿Cuántos cuadrados ves?" que se ve en las preparatorias en CDMX no solo es un reto visual entretenido, sino también un ejemplo fascinante de cómo la matemática subyace en lo cotidiano. La solución de este problema, al descomponer un cuadrado mayor en cuadrados más pequeños, revela una estructura matemática elegante: el número total de cuadrados puede expresarse como la suma de los cuadrados de números naturales consecutivos. Este resultado no es una coincidencia, sino una propiedad inherente a la forma en que los cuadrados se construyen y agrupan.
ResponderEliminarMe pareció un ejercicio visual muy entretenido y desafiante. Este tipo de acertijos son geniales para entrenar la percepción y el pensamiento lógico. ¡Siempre es divertido poner a prueba la mente con retos matemáticos como este!
ResponderEliminar_______________________________________________
Conoce las programas de Licenciaturas Ejecutivas