¿Cuántos triángulos ves?

Tengo la suerte de disfrutar de un elenco de alumnos en 1º de ESO, que comparten conmigo el gusto por la resolución de problemas, haciendo suya la frase "a los matemáticos no nos gustan los problemas, si no que nos divertimos intentando resolverlos". En esta línea, el pasado jueves trajeron un problema a clase y lo plantearon al grupo (incluido al que escribe), y el enunciado del mismo es el que da título a esta entrada: ¿Cuántos triángulos ves?

No cuesta mucho esfuerzo realizar el conteo de los mismos, para darse cuenta que en total hay 24 (es por si solo un ejercicio que recomiendo a cualquiera que le apetezca disfrutar un rato en el intento).

Pero lo que me parece más atrayente es encontrar un método que permita saber de antemano cuántos hay buscando patrones. En esta figura, aparecen dos tipos:

Tipo 1:

Se trata de un triángulo en el que hemos trazado paralelas a la base desde puntos de los lados que no la contienen. Claramente, habrá tantos triángulos como paralelas más el original. De esta forma, si hemos trazado n paralelas, el número de triángulos será .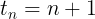

Tipo 2:

Es el más jugoso en cuanto a las cuentas y además el número de triángulos que aparecen es también recursivo, pues al añadir una nueva ceviana (recta que parte de un vértice e incide sobre el lado opuesto) el número de triángulos será la suma de los obtenidos con una ceviana menos y los nuevos que se formen. Para fijar ideas, llamando 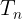 al número de triángulos que aparecen al trazar n cevianas tenemos:

 

Si observamos los primeros valores (1, 3, 6, 10, 15,...) podemos comprobar que la sucesión, es una progresión aritmética de segundo orden con diferencia 1, con lo que el término general vendrá dado por:

Vamos a usar el Principio de inducción para probar esta afirmación sobre el término general:

• Para 
• Supongamos cierto para un natural n que 
• Queremos comprobar que: 

De esta forma: 

Lo que prueba la afirmación sobre el término general (nótese que n+2 es el número de triángulos nuevos que surgen al tratar una ceviana más).

Volviendo sobre la propuesta inicial, nuestra figura está compuesta de dos de tipo 1 (los triángulos FGA y AGC) y tres de tipo 2 (los triángulos BFG, BAG y BAC), con lo que podemos contrastar que el número de triángulos es:

Este post participa en la Edición 7.X del Carnaval de Matemáticas cuyo anfitrión es el Blog del IMUS.